|
PAGE |
QUOTEs
(Most quotes verbatim Henri Louis
Bergson, some paraphrased.) |
COMMENTs
(Relevant to Pirsig, William James
Sidis, and Quantonics Thinking Modes.) |
|
75 |
"NUMBER may be defined
[classically] in general as a collection of units, or, speaking
more
| What is [definition
of] number? |
exactly, as the synthesis of the
one and the many. Every number is one, since it is brought before
the mind by |
a simple intuition and is given a name; but the unity
which attaches to it is that of a sum, it covers a multiplicity
of parts which can be considered separately."
Note (1): I had already
completed the present work when I read in the Critique
Philosophique (for 1883 and 1884) F. Pillon's
very remarkable refutation of an interesting article
by G. Noël on the interconnexion
of the notions of number and space.
But I have not found
it necessary to make any alterations in the following pages,
seeing that Pillon does not
distinguish between time
as quality and time as quantity, between the [conscious]
multiplicity of juxtaposition and that of interpenetration.
Without this vital distinction, which it is the chief aim of
the present chapter to establish, it would be possible to maintain,
with Pillon, that number may be built
up from the relation of co-existence. But what is
here meant by co-existence? If the co-existing terms form
an organic whole, they will never lead us to the notion of [classically
lisr] number;
if they remain distinct, they are in juxtaposition and we are
dealing with space. It is no
use to quote the example of simultaneous impressions received
by several senses. We either leave these sensations their specific
differences, which amounts to saying that we do not
count them; or else we eliminate their differences, and then
how are we to distinguish them if not
by their position or that of their symbols? We
shall see that the verb "to distinguish" has two meanings, the
one qualitative,
the other is quantitative: these two meanings have been confused, in
my opinion, by the philosophers who have dealt with the relations
between number and space.
Return to top of page footnote reference.
|
(Our brackets, bold, color, and violet bold italic problematics.)
Bergson restarts his footnote counts on each page. So to refer
a footnote, one must state page number and footnote number.
Our bold and color highlights follow a code:
- black-bold - important to read if you are just scanning
our review
- orange-bold - text ref'd
by index pages
- green-bold - we see Bergson
suggesting axiomatic memes
- violet-bold - an apparent
classical problematic
- blue-bold - we disagree
with this text segment while disregarding context of Bergson's
overall text
- gray-bold - quotable
text
- red-bold - our direct
commentary
Similarly to Bergson's manner of starting topic 15, he amazes
us here too! He infers a quantum reality where:
Time quanton(quality,quantity),
and quanton(quality,quantity),
and
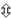 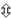
quanton(subjective_wave,objective_particle)
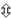 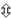
Time quanton(interpenetration,juxtaposition),
where quanton(interpenetration,juxtaposition),
where
interpenetration is n¤nactuality's c¤mplementary
included-middle mediation of multiple comtextual juxtapositions
(AKA interrelationships).
We offer some number heuristics based upon his statements
about time:
- number is quantum
comtextually
dependent via mediating juxtaposition,
- number is quantum associative commingling via mediating interpenetration,
and
- number is quantum animate as a quanton of both quality and
quantity.
Com(n)sider how these three heuristics satisfy Bergson's earlier
statements about two classical delusions of reality:
- that reality is stable, and
- that objects in reality are independent.
See our One is the Onliest
Number.
Com(n)sider how we can proffer similar quantum analogues for
classical concepts of space and mass.
Too, here, we see that, to Bergson, particulate (lisr)
objectivity and space are analogous concepts. He shows
us how durational (quantum real) reality is classically
n¤nnumerable.
Index
|
| 76 |
"Without attempting for the present any thorough examination
of these conceptions of unity and multiplicity,
let us inquire whether the idea of number does not imply
the representation of something else as well.
"It is not
enough to say that number is a collection of units; we must add
that these units are
| The units
which make up a number must be identical. |
identical
with one another, or at least that they are assumed to be identical when they are counted. No doubt we can count the
sheep |
in a flock and say that there are fifty, although
they are all different from one another and are easily recognized
by the shepherd: but the reason is that we agree in that
case to neglect their individual differences and to take into
account only what they have in common. On the other hand, as
soon as we fix our attention on the particular features of objects
or individuals, we can of course make
an enumeration of them, but not
a total [because each sheep
is unique/omnifferent]. We place ourselves at these two very
different points of view when we count the soldiers
in a battalion and when we call the roll. Hence
we may conclude that the idea of number implies the simple intuition
of a multiplicity of parts or units, which are absolutely
alike."
|
(Our brackets, bold, color, violet bold italic problematics,
and bold italic problematics.)
In Quantonics, in general, we deny any classical concepts
of identity and identicalness!
Also see difference,
omnifference,
and one.
In quantum reality, what we can do (theoretically)
is make a Bose-Einstein Con(m)densate (BEC) of them. In such
a case, all 'objects' would share common quantum phasicities.
In a sense many classical 'objects' could become ¤ne quantum
co-here-nt quanton. Comsider how BECs eliminate quantonic interrelationships
among condensed quantons. This process is ~reversible; however,
when 'reversed' each classical 'object' would, initially share
common quantum phasicities as ensemble "absolutely
alike" initial comditions which would then, at
up to Planck-rates, evolve omnifferently from thence on.
Bergson apparently did n¤t anticipate our quantum description
above. He just said that since all sheep are, indeed, quantumly
omnifferent ¤ne another, we cann¤t classically
total them, ideally-mathematically, as a sum of cloned identical
classical numeric units. Ten sheep as a total is n¤t ten
classically 'identical' sheep!
Index
|
| 77 |
"And yet
they must be somehow distinct from one another, since
otherwise they would merge
| But they must
also be distinct. |
into a
single unit. Let us assume that all the sheep in the
flock are identical; they
differ at least by the position which they occupy in |
space, otherwise they would not
form a flock. [Bergson's argument here is analogous one we used
in our One is the Loneliest page.]
But now let us even set aside the fifty sheep themselves and
retain only the idea of them. Either we include them all in the
same image, and it follows as a necessary consequence that we
place them [classically] side by side in an ideal [classical]
space, or else we repeat fifty times in succession the image
of a single one, and in that case it does seem, indeed, that
the series lies in duration rather than in space. But we shall
soon find out that it cannot be so. For if we picture to ourselves
each of the sheep in the flock in succession and separately,
we shall never have to do with more than a single sheep. In order
that the number should go on increasing in proportion as we advance,
we must retain the successive images and set them alongside each
of the new units which we picture to ourselves: now, it
is in space that such a juxtaposition takes place and
not in pure duration.
In fact, it will be easily granted that counting material objects
means thinking all these objects together, thereby leaving them
in space. But does this intuition of
space accompany every idea of number, even of an abstract
number?" |
(Our link, bold, color, and violet bold italic problematics.)
Now we see Bergson actually anticipate BECs! Taken literally,
Bergson's "merge into a single
unit" is quantum coherence, or more specifically
Bose-Einstein Con(m)densation (BEC).
Can you see what an impact this has on classical mathematics?
All numerical sums,
to be quantum physially real, must represent BECs! Personally,
we had never intuited that Bergsonian meme prior to now (16Apr2002).
Index
|
| 78 |
"Any one can answer this question
by reviewing the various forms which the idea of number has
| We cannot form an image or
idea of number without the accompanying intuition of space. |
assumed for him since his childhood.
It will be seen that we began by imagining e.g. a row of balls,
that these balls afterwards became points, and, finally, this
image itself disappeared, leaving behind it, as we say, nothing
but |
abstract number. But at this very moment we ceased
to have an image or even an idea of it; we kept only the symbol
which is necessary for reckoning and which is the conventional
way of expressing number. For we can confidently assert
that 12 is half of 24 without thinking either the number 12 or
the number 24: indeed, as far as quick calculation is
concerned, we have everything to gain by not
doing so. But as soon as we wish to picture number to
ourselves, and not
merely figures or words, we are compelled to have recourse
to an extended image. What leads to misunderstanding on this
point seems to be the habit we have fallen into of counting
in time rather than in space. In order to imagine the number
50, for example, we repeat all the numbers starting from unity,
and when we have arrived at the fiftieth, we believe we have
built up the number in duration and in duration only. And
there is no doubt that in this way we have counted
moments of duration rather than points in space; but the
question is whether we have not counted the moments of duration by means of
points in space." |
(Our bold and color, and violet bold italic problematics.)
But, but, but, ... Einstein has told us time and space are
identical!!! He said, "Reality
is a space-time identity!" Is this what Feynman and Dyson
meant when they conjectured Einstein had become a manipulator
of mathematics and numbers and thus had lost touch with concrete
(i.e. real) physical reality?
In quantonics, we can easily answer this issue using QTMs.
All pairs of meme interrelationships in quantonics are quantons.
All quantons are uncertainty interrelationships. So we just say,
"quanton(time,space)." Spaces always have temporalities
and temporalities always have spaces. How much of each depends
upon which we are attempting to measure. This meme is
analogous a Poisson bracket of a quanton's position and momentum.
Space and time are quantum c¤mplementary!
Quantons are paired quantum c¤mplementary interrelationships!
We can use them to express general quantum systems, because general
quantum systems are nestings of animate quantum c¤mplementary
interrelationships.
|
| 79 |
"It is certainly possible to
perceive in time, and in time only, a succession which is nothing
but a succession, but not
an addition, i.e. a succession which culminates in a sum. For
though we reach a sum by taking into account a succession of
different terms, yet it is necessary that each of these terms
should remain when we pass to the following, and should wait,
so to speak, to be added to the others: how could it
wait, if it were nothing but an instant of duration? And
where could it wait if we did not
localize it in space? We involuntarily fix at a point in space
each of the moments which we count, and it is only on this condition
that the abstract units come to form a sum. No doubt it is
possible, as we shall show later, to conceive the successive
moments of time independently of space; but when we add to the
present moment those which have preceded it, as is the case when
we are adding up units, we are not
dealing with these moments themselves, since they have vanished
for ever, but with the lasting traces which they seem to have
left in space on their passage through it. It is true that
we generally dispense with this mental image, and that, after
having used it for the first two or three numbers, it is enough
to know that it would serve just as well for the mental picturing
of the others, if we needed it. But every clear idea of number
implies a visual image in space; and the direct study of the
units which go to form a discrete multiplicity will lead us to
the same conclusion on this point as the examination of number
itself." |
(Our brackets, bold, color, and violet bold italic problematics.)
Here, via his "...in time only," Bergson denies
our view of quantonic uncertainty interrelationships among measurables
in reality. Doesn't this deny his own statements about classicists'
two greatest delusions that:
1) reality is stable, and
2) objects in reality are independent?
But then he shows us how "terms" in duration are
unstoppable. (Note how a classical concept of "waiting"
AKA "stoppability" is necessary for mathematical induction,
which is at heart of Peano's counting principle which Bergson
is discussing here. Unstoppable duration (quantum reality) is,
as we have shown elsewhere and as Bergson is showing us in his
works, n¤n-inductive, n¤ndeterministic, and thus
n¤ncausal!)
Study that link carefully! Doug - 25Mar2004.
We might use photographs as cinematographical analogies here.
They do n¤t really make duration "wait,"
either! We just tend to classically thingk
that they do. Classical scientists do exactly this with their
mathematics and their measurement and their digital computers!
All they do is take 'photographs' of reality, process those 'photographs'
analytically, state-ically,
dichotomously, anachronistically, inanimately and call their
results "real."
Index
|
| 80 |
"Every number is a collection
of units, as we have said, and on the other hand every number
is itself
| All unity
is the unity of a simple act of the mind. Units
divisible only because regarded as extended in space. |
a unit,
in so far as it is a synthesis of the units which compose it. But
is the word unit taken in the same sense in both cases?
When we assert that number is a unit, we understand by this that
we master the whole of it by a simple and indivisible intuition
of the mind; |
this unity thus includes a multiplicity,
since it is the unity of a whole. But when we speak of the units
which go to form number, we no longer think of these units as
sums, but as pure, simple,
irreducible units, intended to yield the natural
series
of numbers by an indefinitely continued process
of accumulation. It seems, then, that there are two
kinds of units, the one ultimate, out of which a number is formed
by a process of addition, and the other provisional, the number
so formed, which is multiple in itself, and owes its unity to
the simplicity of the act by which the mind perceives it. And
there is no doubt that, when we picture the units which make
up number, we believe that we are thinking of indivisible components:
this belief has a great deal to do with the idea that it is possible
to conceive number independently of space. Nevertheless, by looking
more closely into the matter, we shall see that all unity is
the unity of a simple act of the mind, and that, as this is an
act of unification, there must be some multiplicity for it to
unify." |
(Our bold and color.)
Quantum reality is n¤t classically synthetic.
It is, rather, durationally emerging.
Classical number exclusively complements unity and
multiplicity; however, classical number denies quantum requisite
c¤mplementarity of animacy and inanimacy (quantum requisite
absence of classical stability), and quantum requisite c¤mplementarity
of included-middle and excluded-middle (quantum requisite absence
of "exclusive" classical objective independence). To be able to understand and differentiate classical
reality from quantum reality, we cann¤t over emphasize
importance of what we just wrote! Doug - 17Apr2002.
Index
|
| 81 |
"No doubt, at the moment at
which I think each of these units separately, I look upon it
as indivisible, since I am determined to think of its unity alone.
But as soon as I put it aside in order to pass to the next, I
objectify it, and by that very deed I make it a thing, that is
to say, a multiplicity. To convince oneself of this, it is
enough to notice that the units by means of which arithmetic
forms numbers are provisional units, which can be subdivided
without limit, and that each of them is the sum of fractional
quantities as small and as numerous as we like to imagine. How
could we divide the unit, if it were here that ultimate unity which characterizes a simple
act of the mind? How could we split it up into fractions whilst
affirming its unity, if we did not
regard it implicitly as an extended object, one in intuition
but multiple in space? You will
never get out of an idea which you have formed anything which
you have not put into it; and if the unity by means of which you make
up your number is the unity of an act
and not of an object,
no effort of analysis will bring out of it anything but unity
pure and simple. No doubt, when you equate the number 3 to the
sum of 1 + 1 + 1, nothing prevents you from regarding the units
which compose it as indivisible: but the reason is that
you do not choose
to make use of the multiplicity which is enclosed within each
of these units. Indeed, it is probable that the number 3 first
assumes to our mind this simpler shape, because we think rather
of the way in which we have obtained it than of the use which
we might make of it." |
(Our brackets, bold, color, and violet bold italic problematics.)
Index
|
| 82 |
"But we soon perceive that, while all multiplication
implies the possibility of treating any number whatever as a
provisional unit which can be added to itself, inversely the
units in their turn are true numbers which are as big as we like,
but are regarded as provisionally indivisible for the purpose
of compounding them with one another. Now, the very admission
that it is possible to divide the unit into as many parts as
we like, shows that we regard it as extended.
"For we must understand what is meant by the discontinuity of
number. It cannot be denied
| Number in process
of formation is discontinuous but, when
formed, is invested with the continuity of space. |
that the formation
or construction of a number
implies discontinuity. In
other words, as we remarked above, each of the units with which
we form the number 3 seems to be indivisible while
we are dealing with it, and we pass abruptly from
one to |
the other. Again, if we form the same number with halves,
with quarters, with any units whatever, these units, in so far
as they serve to form the said number, will still constitute
elements which are provisionally indivisible, and it is always
by jerks, by sudden jumps, so to speak, that we advance from
one to the other. And the reason is that, in order to get a number,
we are compelled to fix our attention successively on each of
the units of which it is compounded."
|
(Our brackets, bold and color.)
Index
|
|
83 |
"The indivisibility of the
act by which we conceive any one of them is then represented
under the form of a mathematical point which is separated from
the following point by an interval of space. But, while a
series of mathematical points arranged in empty space expresses
fairly well the process by which we form the idea of number,
these mathematical points have a tendency to develop into lines
in proportion as our attention is diverted from them, as if they
were trying to reunite with one another. And when we look at
number in its finished state,
this union is an accomplished fact: the points have become
lines, the divisions have been blotted out, the whole displays
all the characteristics of continuity. This is why
number, although we have formed it according to a
definite law, can be split up on any
system we please. In a word, we must distinguish
between the unity which we think of and the unity which we set
up as an object after having thought of it, as also between number in process of formation and number
once formed. The unit is irreducible
while we are thinking it and number is discontinuous while we
are building it up: but, as soon as we consider number in its
finished state, we objectify it, and it then appears to
be divisible to an unlimited extent. In fact, we apply the term
subjective to what seems
to be completely and adequately known, and the term objective to what is known in such
a way that a constantly increasing number of new impressions
could be substituted for the idea which we actually have of it." |
(Our brackets, bold, color, violet bold italic problematics,
and violet bold problematics.)
dichon(continuity,
discontinuity)
Quantum real emergent number! In "...process of formation."
Classical unreal state-ic
number, "...once formed."
Index
|
| 84 |
"Thus, a complex feeling will contain a fairly large
number of simple elements; but, as long as these elements do
not stand out with
perfect clearness, we cannot
say that they were completely realized, and, as soon as consciousness
has a distinct perception of them, the psychic state
which results from their synthesis will have changed
for this very reason. But there is no change in the general appearance
of a body, however it is analysed by thought, because these different analyses, and an infinity
of others, are already visible in the
mental image which we form of the body, though they
are not realized:
this actual and not
merely virtual perception of subdivisions in what is undivided
is just what we call objectivity.
It then becomes easy to determine the exact
part played by the subjective and the objective in the idea of number. What properly
belongs to the mind [quantum stage] is the indivisible
process by which it concentrates attention successively on the
different parts of a given space; but the parts which have thus
been isolated [quantum islandicity] remain in order to
join [quantum included-middle holism] with the others,
and, once the addition is made, they may be broken up in any
way whatever. They are therefore parts of space, and space
is, accordingly, the material, with which
the mind builds up number, the medium in which the
[classical] mind places it.
"Properly speaking, it is arithmetic
which teaches us to split up without
limit the units of which number consists. Common
sense is very much inclined to build up number with indivisibles."
|
(Our brackets, bold, color, violet bold italic problematics,
and violet bold problematics.)
Here, Bergson offers us his rendition of quantum uncertainty.
It is analogous a Poisson bracket of change
and perfect clarity.
Classically:
dichon(subjective_opposite, objective_opposite)
Quantumly:
quanton(subjective_c¤mplement,objective_c¤mplement)
Bergson explains how we impose tendentious classicism on a
quantum reality.
Bergson explains a source classicism's grand delusion of analytic
reducibility: "...a cuisinart is our best means of
understanding biological constructs."
Readers might also wish to comtemplate
our take on classical "common sense." Doesn't common
sense imply that we all have to think alike in order to agree
on what we observe? Isn't common sense an analogue of mental
cloning? What do modern academic institutions all do at Millennium
III's commencement? Don't they do their best to clone minds on
various subjects?
Isn't it classically considered good that classical
'scientists' all share one paradigm, one disciplinary matrix,
one set of exemplar hermeneutics?
Would any truly extraordinary and pioneering scientist ever
want his-her mind cloned or to be/have a cloned mind of a socially
constructed paradigm?
Cloned minds are but ideal social concepts.
If we want our cultures to be diverse, why would we not want
minds within our paradigms to be 'diverse.' We must realize that
paradigms are state-ic patterns of social value, and as such,
and happily, they are their own worst threat to survival.
We believe that social value AKA "common sense"
should seldom be permitted to rule intellectual, intuitional,
and instinctual patterns of value! Resist, yæs!
Rule n¤! Fortunately, it does n¤t and ultimately
it cann¤t.
One more comment: "Common sense," to us,
is font and grail of denigration trumpeted against novel
memes and their pioneers who threaten those trapped in devolving
paradigms. Those trapped call their threats, "...idiots,
insane, fools, charlatans, fraudulent, equivocal, prevaricative,
liars, etc." When we hear those denigrations, we know those
emitting such denigrations are, indeed, weak and fearful. Extraordinary
scientists understand that n¤vel memes are precursors
of exceptional scientific breakthroughs.
See our review of Thomas Kuhn's The
Structure of Scientific Revolutions.
Index
|
| 85 |
"And this is easily understood, since the provisional
It follows that number is actually
thought of as
a juxtaposition in space. |
simplicity of the component units
is just what they owe to the mind, and the latter pays more attention
to its own acts than to the material on which it works. Science
confines itself, here, |
to drawing our attention to this material: if we did
not already localize number
in space, science would certainly not
succeed in making us transfer it thither. From the beginning,
therefore, we must have thought of number
as of a juxtaposition in space. This is the conclusion
which we reached at first, basing ourselves on the fact that
all addition implies a multiplicity
of parts simultaneously perceived.
"Now, if this conception of number is granted, it will
be seen that everything is not
counted in the
Two kinds of multiplicity:
(1) material objects,
counted in space;
(2) conscious states, not countable unless symbolically represented
in space. |
same way, and that there are two very different kinds of multiplicity.
When we speak of material objects, we refer to the possibility
of seeing and touching them; we localize them in space. In that
case, no effort of the inventive faculty or of symbolical |
representation is necessary in order to count them; we
have only to think them, at first separately, and then simultaneously,
within the very medium in which they come under our observation.
The case is no longer the same when we consider purely affective
psychic states, or
even mental images other than those built up by means of sight
and touch."
|
(Our brackets, bold, color, and violet bold italic problematics.)
Yes, we agree. In our view, quantum reality shows us that
reality is n¤t substantial, material, objective, spatially
immutable, etc. Rather quantum reality is flux. Space is n¤t
extensible number. Quantum space is flux wavelength!
Quantum space's smallest (currently known) wavelength is what
we call a "Planck length." It apparently limits quantum
flux's maximum frequency, and its minimum wavelength.
Quantum space's longest wavelength is ~unlimited depending
upon whether and how quantum philosophy and science ultimately
discover and decide what most closely represents percept zero
in Nature. It apparently limits quantum flux's minimum frequency,
and its maximum wavelength.
When we grasp quantum
essence that quantum flux is not classically, spatially limited,
we see that a current simple, classical univalent concept
of number derived from it is wholly naïve. And that is just
what Bergson is attempting to show us. We emerse a n¤vel
meme that any quantum number is omnivalent. We might even think
of quantum number as a qubit. E.g., an atom may be QTM-thought
of as a qubit of qubits (e.g., its electrons and nuclei).
Bottom line: a naïve concept of classical
number is innately
incapable of representing a quantum reality whose quantons' numbers
are essentially omnivalent qubits.
Index
|
| 86 |
"Here, the terms being no longer
given in space, it seems, a priori, that we can hardly
count them except by some process of symbolical representation.
In fact, we are well aware
of a representation of this kind when we are dealing with sensations
the cause of which is obviously situated in space. Thus, when
we hear a noise of steps in the street, we have a confused vision
of somebody walking along: each of the successive sounds
is then localized at a point in space where the passer-by might
tread: we count our sensations
in the very space in which their tangible causes are ranged.
Perhaps some people count the successive
strokes of a distant bell in a similar way, their
imagination pictures the bell coming and going; this spatial
sort of image is sufficient for the first two units, and the
others follow naturally. But most people's [classical] minds
do not proceed in
this way. They range the successive sounds in an ideal space
and then fancy that they are counting them in pure duration.
Yet we must be clear on this point. The sounds of the bell certainly
reach me one after the other; but one of two alternatives must
be true. Either I retain each of these successive sensations
in order to combine it with the others and form a group which
reminds me of an air or rhythm which I know: in that case
I do not count
the sounds, I limit myself to gathering, so to speak, the qualitative
impression produced by the whole series." |
(Our brackets, bold and color.)
In his Creative Evolution,
Bergson refers this kind of (more quantumesque) think-king as
"...think being directly." See our coined thibedir.
Index
|
| 87 |
"Or else I intend explicitly
to [classically] count them, and then I shall have to [classically]
separate them, and this separation must take place within some
[classically] homogeneous medium in which the sounds, stripped
of their qualities, and in a manner emptied, leave traces of
their presence which are [classically] absolutely alike. The
question now is, whether this medium is time or space. But
a moment of time, we repeat, cannot persist in order to be added
to others. If the sounds are separated, they must leave empty
intervals between them. If we count
them, the intervals must remain though the sounds disappear:
how could these intervals remain, if they were pure duration and not
space? It is in space, therefore, that the operation takes
place. It becomes, indeed, more and more difficult as we penetrate
further into the depths of consciousness. Here we find ourselves
confronted by a confused multiplicity of sensations and feelings
which analysis alone can distinguish. Their number is identical with the number of the
moments which we take up, when we count
them; but these moments,
as they can be added to one another, are
again points in space. Our final
conclusion, therefore, is that there are two kinds of multiplicity:
that of material objects, to which the conception of number is
immediately applicable; and the multiplicity
of states
of consciousness, which cannot be regarded as
numerical without the help of some symbolical representation,
in which a necessary element is space." |
(Our brackets, bold and color, violet bold italic problematics,
and violet bold problematics.)
As we said above, "this medium" is pragmabsolute
quantum flux. We can show that space, time, mass, and gravity
are all functions of quantum flux. Bergson did n¤t
k-now this. (Our use of "k-now" is quantonics lingo
for Bergson's "...think being directly..." and our
comtraction of it: thibedir. Where classicists 'know'
via classical reality's state-ic, rote information on yuck-stuck
status quo is the way to go know-ledges, students of Quantonics
are k-now-ing via direct experience of an animate, plural, c¤mplementary
quantum reality.)
Bergson's "two kinds of multiplicity" are
still both classical since they are both spatial. To extend his
kinds of multiplicity into a quantum realm we must first realize
that quantum flux is crux. Then we can begin to fathom that,
in a sense, quantum reality is unlimited multiplicity —
beyond any naïve classical categorization.
Index
|
| 88 |
"As a matter of fact, each
of us [classically] makes a distinction between these two kinds
of multiplicity
| The impenetrability of matter is
not a physical but a logical necessity. |
whenever he speaks of the impenetrability of matter. We sometimes
set up impenetrability as
a fundamental property of bodies, known in the same way and put |
on the same level as e.g. weight or resistance. But
a purely negative [classical] property of this kind cannot be
revealed by our senses; indeed, certain experiments in mixing
and combining things might lead us to call it in question if
our minds were not already
made up on the point. Try to picture one body penetrating
another: you will at once assume that there are empty
spaces in the one which will be occupied by the particles of
the other; these particles in their turn cannot penetrate one
another unless one of them divides in order to fill up the interstices
of the other; and our thought will prolong this operation indefinitely
in preference to picturing two bodies in the same place. Now,
if impenetrability were really
a quality of matter which
was known by the senses, it is not
at all clear why we should experience more difficulty in conceiving
two bodies merging into one another than a surface devoid of
resistance or a weightless fluid. In reality, it is not a physical but a logical
necessity which attaches to the proposition "Two
bodies cannot occupy the same place at the same time."
The contrary assertion involves an [classical] absurdity which
no conceivable experience could succeed in dispelling." |
(Our brackets, bold and color, and violet bold italic problematics.)
Impenetrability is a classical
code word for Aristotle's
excluded-middle. Classical impenetrability
describes SOM's wall. But as students of Quantonics, we k-now
that Quantum flux compenetrates quantum flux. Thus quantum reality
is, indeed, penetrable. William James would say it is "compenetrable."
Fritjof Capra would say it is "interpenetrable." Sadly,
classicists, though they refer themselves 'scientists,' are just
like us naught but amateurs on Nature's quantum real stage. Decline
and fall of their ugly classical deign to feign is nigh. A quantum
tsunami of Millennium III change shall wash our Earth clean of
them. Doug - 18Apr2002.
And here, Bergson implies that classical logic misinterprets
physical (to us, physial) reality. If that is what he
intends, then we agree. Of course, reader, you understand that
Quantonics denies classical syllogistic logic as n¤nquantum.
Quantum Bose-Einstein Condensation physically demonstrates, "[~Unlimited] bodies [can] occupy the
same place at the same time."
Index
|
| 89 |
"In a word, it implies a [classical]
contradiction. But does not this amount to recognizing
that the very idea of the number 2, or, more generally, of any
number whatever, involves
the idea of juxtaposition
in space? If impenetrability
is generally regarded as a quality of
matter, the reason is that the idea of number is
thought to be independent of the idea of space. We thus believe
that we are adding something to the idea of two or more objects
by saying that they cannot occupy the same place: as if
the idea of the number 2, even the abstract number, were not already, as we have shown,
that of two different positions in space! Hence
to assert the impenetrability of
matter is simply to recognize
the inter-connexion between the notions of number and space,
it is to state
a property of number rather than of
matter.—Yet, it will be said, do we not count
feelings, sensations, ideas, all of which permeate
one another, and each of which, for its part, takes up the whole
of the soul?—Yes, undoubtedly; but, just because they
permeate one another, we cannot count them unless we represent
them by homogeneous units which occupy separate positions in
space and consequently no longer permeate one another. Impenetrability thus makes its appearance at
the same time as number [Classical impenetrability
depends upon a concept of Aristotelian excluded-middle; this
concept is necessary for classicists to assure objective, numerical
non-contradiction. But reality
is not classical!
Reality is quantum Quantum reality's middle is included! Reality's
quantons are not just
penetrable, they are interpenetrable!] ; and when we attribute
this quality to matter in order to distinguish it from everything
which is not matter [remember,
Bergson has already shown us that classical negation,
'not' is subjective], we simply state
under another form the distinction established above between
extended objects, to which the conception of number is immediately
applicable, and states
of consciousness, which have first of all to be represented symbolically
in space." |
(Our brackets, bold and color, and violet bold italic problematics.)
Here, Bergson puts us in pure awe of him! This is so beautiful,
so prescient, so quantum...
If matter is impenetrable and we use number to describe
and measure matter, then how can number be penetrable? If number
is impenetrable, how can scientists use number to do sums and
products, both of which we may view as penetrable quantum condensates
of classically physical description? Heads up, readers! Doug
- 18Apr2002.
Amazing! Bergson shows us that concepts of classical
number, and classical material impenetrability classically contradict
one another! Simply Awesome! Wow!
Why has science ignored this immense classical problematic!
We have not tumbled to this Bergsonian perspective prior to now.
To us, this is an outright denial of classical material science
and its 'valid' uses of classical mathematics. Also, we see this
as another tell of reality's underlying quantum nature.
Index
|