matter to get such a theory....One can get a much simpler theory if one goes over to the
corresponding classical mechanics, which is the form which quantum mechanics takes
when one makes Planck's constant
| U = |
|
|
|
|
|
|
|
I = |
|
|
|
|
|
|
|
J = |
|
|
|
|
|
|
|
K = |
|
|
|
|
|
|
 |
||
 |
2q | ||
|
iq2q |
|||
  |
||||
|
1q = |
Compare our usage of Classical Equals to Quantonic Equalings5 |
  |
||
|
Equals - "No Bell Inequalities permitted!" |
Equalings - "Bell Inequalities expected as quantum ubiquitous!" |
|||
|
'the single most powerful argument for the use of a non-classical logic in quantum mechanics.'" a probability should be assigned to every element of the [quantum]algebra of event[processe]s..." p. 359, Max Jammer, The Philosophy of Quantum Mechanics. (Our brackets and italicization of thelogos.) 'The probabilistic argument for a non-classical logic of quantum mechanics,' Philosophy of Science 33, 14-21 (1966), P. Suppes. 'the only convincing argument' for quantum logic..." p. 360, Jammer. TPoQM. Our approach is to assign potentia for unlimited probabilities and likelihoods to each quanton's interrelationships. We do this using quantonics' fuzzons. We offer a novel quantonics' fuzzons to fermion ontology for your consideration. A Primer on Quantum~Cuneiform's graphic entitled 'A Reservoir of Wave Functions.' |
||||
  |
  |
|||
| 0q | |
-q | ||
  |
  |
|||
|
2q |
|
+q | ||
|
|
|
|
||
|
|
|
|||
|
|
 |
|
||
|
|
|
 |
||
|
|
|
|
||
 |
2q |
|
||
|
|
|
 |
||
 |
|
|||
Notes:
1 - Hamilton's "hypercomplexity" illustrates quantum reality's own heterogeneity. It shows a second set of complex variables. Both are what we call "conjugates." It does n¤t show Quantonics' quantum comjugation, which requires, as we show above, introducing real quantum subjectivity. Of course, introducing quantum subjectivity breaks all classical rules which depend upon classical immutability/stability/stoppability (except for unitemporal objective motion), and classical Aristotelian/EEMD/Sheffer-stroke-binary-alternative-denial/lisr classically-negatable, contradictable objective independence.
2 - What we have done here is apply Quantonic
n¤mbærs
to Hamilton's quaternions in their ![]() representation (each of U, I, J, K are two-space planes
and hyperplanes; their combination is three-space hyper volumes).
Our approach is applicable in
representation (each of U, I, J, K are two-space planes
and hyperplanes; their combination is three-space hyper volumes).
Our approach is applicable in ![]() too, where matrices
become 4 by 4. Dirac used
too, where matrices
become 4 by 4. Dirac used ![]() to develop his
relativistic version of QED. Indeed, that was Dirac's own epiphany:
to use
to develop his
relativistic version of QED. Indeed, that was Dirac's own epiphany:
to use ![]() to solve QED relativity problems which
flummoxed Pauli. See Tomonaga's Lecture 3 in his The Story
of Spin, 1997 (translation), UChicP. Please realize that all
of Pauli's and Dirac's accomplishments were purely classical.
Perhaps what is most interesting to us is a general classical
bias that physicists and mathematical physicists then felt it
necessary to relativize quantum theory, but not to quantize relativity
theory... Is that bias because relativity came first? We think
so. Beware unitemporal classical cohesion (essentially classical
cause-effect
induction). Einstein's celebrity pulled lots of wool and paradigmatically
disciplined lots of blinders. Beware celebrity! Too, beware Einsteinian
classical relativity!
to solve QED relativity problems which
flummoxed Pauli. See Tomonaga's Lecture 3 in his The Story
of Spin, 1997 (translation), UChicP. Please realize that all
of Pauli's and Dirac's accomplishments were purely classical.
Perhaps what is most interesting to us is a general classical
bias that physicists and mathematical physicists then felt it
necessary to relativize quantum theory, but not to quantize relativity
theory... Is that bias because relativity came first? We think
so. Beware unitemporal classical cohesion (essentially classical
cause-effect
induction). Einstein's celebrity pulled lots of wool and paradigmatically
disciplined lots of blinders. Beware celebrity! Too, beware Einsteinian
classical relativity!
3 - As we have shown elsewhere in Quantonics,
when we say "real" that statement issi n¤t an
analogue of saying
"reality." Simply, real issi n¤t reality.
Why? We can use Quantonic script to show you: reality![]() quantons(reals'_complements,reals)
which is very much like saying reality
quantons(reals'_complements,reals)
which is very much like saying reality![]() quantons(n¤nactuality,actuality),
latter which most students of Quantonics are exceptionally familiar
by now. See our real
table entry in our review of EPR's paper EPR (large
page).
quantons(n¤nactuality,actuality),
latter which most students of Quantonics are exceptionally familiar
by now. See our real
table entry in our review of EPR's paper EPR (large
page).
4 - As we have impressed on students of
Quantonics elsewhere and frequently, classicists tend to use classical
concepts to make quantum reality go away, and make quantum reality
classically 'real.' Taking ![]() to zero is taking
quantum reality to classical reality. See our relevant July, 2001
Flash commentary on classical
'gauge invariance.'
to zero is taking
quantum reality to classical reality. See our relevant July, 2001
Flash commentary on classical
'gauge invariance.'
Least energy action e issi 2q•![]() q•
q•![]() q.
Said Hamiltonian quaternion is an action representation. Zeroing
q.
Said Hamiltonian quaternion is an action representation. Zeroing
![]() zeroes and disables quantum action. It removes quantum
flux from all classical notation and thing-king. It, simply, is
n¤n-quantum-real. Notice how our better (yet still
wanting, always wanting) Quantonics approach anihmatæs
our representation of quantum action in its Hamiltonian quaternion
emerqancy. Doug - 28Jun2003.
zeroes and disables quantum action. It removes quantum
flux from all classical notation and thing-king. It, simply, is
n¤n-quantum-real. Notice how our better (yet still
wanting, always wanting) Quantonics approach anihmatæs
our representation of quantum action in its Hamiltonian quaternion
emerqancy. Doug - 28Jun2003.
5 - Students of Quantonics may find it worthwhile to experience an epiphany that Quantonics' equalings are all "Bell inequalities." Indeed, all quantum n¤mbærs, all quantons, according to Quantonics' beliefs, are essentially quantum c¤mplementary "Bell inequalities." Bell's inequalities, as he propounded them, are classically presumed inanimate, excluded-middle, and state-ic. Naïve AKA "local" realists (classicists) insist upon a classical notional ideal 'equality' akin Aristotle's first syllogism, A=A. So finding inequalities, to a classicist, is a BIG surprise! Of course our equalings are anihmatæ, EIMA quantons. What makes "Bell's inequalities" inequalities? Quantum reality's intrinsic anihmatæ EIMA. Why is this quantum notion ironic and paradoxical to classicists? They view reality as inanimate, immutable, state-ic, excluded-middle, and everywhere-independent-dissociative!
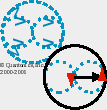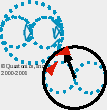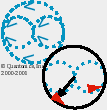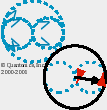
We created another n¤vel graphic which students may use to visualize any quanton's EIMA:
 |
That sphere issi a sphere of p¤tentially (an) ¤mnivalent (ensehmble of) quantum included-middle c¤mma-n¤-space c¤pula. It shows that when we depict quanton(c¤mplementqi,c¤mplementqj), its quantum EIMA c¤mma-n¤-space issi massively heter¤gene¤us. Imagine our quanton's c¤mma-n¤-space c¤pulum as only an iceberg tip of that c¤mma-n¤-space sphere. Then imagine all that as abs¤lutely anihmatæ quantum flux.
Here is an analogous ~circular GIF showing what we intend, in 2D, less abstractly (coarse 30° increments for readability; imagine that disk of c¤mplements being rotated ecliptically too, to make a quasi-sphere, and then anihmatæd):
 |
Here you can see heter¤gene¤us, ensehmble quantum c¤mplements without having to infer their presence only by a spherical 'hive' of c¤mma-n¤-space anihmatæ EIMAs. This is a sort of sledge-hammer way of saying, "There are n¤ classical dyads in quantum reality, and there are n¤ Aristotelian syllogisms in quantum reality. Too, if you fathom what we intend, Bell's inequalities are hologral and thus perpetually~ubiquitous in quantum reality. There are n¤ 'equalities' in quantum reality!" See identity. See equals.
6 - At beginning of section 79 of Dirac's The Principles of Quantum Mechanics he says, "The complete Hamiltonian for electrons and positrons interacting with the electromagnetic field is
T¤ sh¤w this ihn Quantonics scrihpt wæ d¤ this
It's just that simple!
Doug - 10Jul2003-17Feb2005