| |
'equilibria'
'equilibrium'
Etymology - Classical
Etymology - Quantum
Synonyms - Classical
Synonyms - Quantum
|
This QELR
of equilibria and equilibrium is in progress until further
notice - Doug - 20,22,24-30Mar2011 and 1,5,10,12-13,15-16,20-21,24Apr2011,1-13Sep2011.
Begin
a Doug 8Mar2014 Equilibrium vav Classical Definiteness Aside:
For Doug, perhaps his most significant impetus for remediating
equilibria from classical to quantum is a simple classical-notion
(presumption) that equilibriac are (can be)
definite. 'Reasonsc'
for this presumptionc are numerous, but bogus.
Why bogus? They violate a quantum~meme that reality
is quantum~uncertain (stochasticallyq indefiniteq).
Bear in mind: change is absolute and uncertainty is stochastic!
When we thinkq of equilibriaq we must
embrace indeterminationq and reject all other
(quantumly~)bogus "static
classical optimisms." 21Mar2014 rev - Add missing 'reject.'
Add missing link to Kuhn's Structure of Scientific Revolutions.
Doug.
Simply: Quantonics HotMeme™
"All
equilibriaq are
tentativeq, tenuousq,
and indeterminateq
across all quantum
spectra and
their quantum~wave~functions."™
Quantonics
HotMeme™
Definitenessc is a classical apparition!
Equilibriaq are indefiniteq (uncertainq)!
This makes clearer another Doug HotMeme™
"Chaosq masters equilibriaq."™
HotMeme™.
Doug - 8Mar2014.
End a Doug 8Mar2014 Equilibrium vav Classical Definiteness
Aside.
We have a major challenge here in our attempts to remediate
'equilibrium.'
Why? Why remediate equilibrium? Classical 'equilibrium' omniffers
radically quantum~equilibrium. From near end of Doug's online
FEP textbook, Chapter
4, Topic 1, paraphrased for use here, "Key to grasping why
all this is necessary...quantum reality is evolving and all its
relationshipings are n¤nlinear, due quantization
and scintillation, and we need to
be 'saying, writing, doing' capable of moving
into and out of quantum~equilibrium
and show us ways of omnitoring said changes."
Doug - 22Feb2012.
Classical 'equilibrium' assumes immutable, perpetual, absolute,
concrete 'state.' Classical equilibrium assumes reality
can be stopped and analyzed mechanically in 'zero momentum reference
frames,' which themselves have 'equilibrium' of an ideal classical
formality.
Begin a
Doug 26Jul2011 Equilibrium vav Reversibility Aside:
Doug has written, many timings in many placings, a quantum~parable~fable
that, paraphrased,
HotMeme™ "Movement (quantum:
wolf eating said lamb) is radically quantum~absolute,
and Rest
(classical: wolf and lamb as concrete objects) is only a classical
apparition."™ HotMeme™.
In general movement
is absolute, quantumly. Classically and specifically,
when viewed locally
and naïvely, concrete rest only appears 'real.'
Classicists are
"Earth Chauvinists." They believe Earth is 'reality.'
They objectively and concretely deny evolution as absolute.
Why? A static and concrete reality may be conveniently-conventionally
described completely by dialectic.
Trouble is, that's (status quo is) just bogus!
Here is a graphic which shows cosmic proportions and scale
of absolute cosmic movement, and Qycloidal™
quantized, Noun~finalNoun movementings:
A Quantum~Hologramic Cosmic~Metabolic
Quantum~Flux in Cycloidal Motion
Movement
and Rest
Doug - 25-26Jul2011, 22Sep2015.
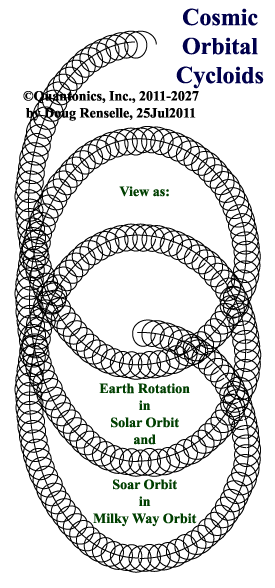 |
 |
When we view that graphic's absolute cycloidal movement as
a m¤dal of Earth's solar system orbit in its milky-way
orbital travels, we have to admit to absolute
motion of all on Earth from any cosmic perspective as moving
in excess of 200 miles per second. Doug believes total motion
is much greater than that, perhaps thousands of miles per second.
Doug assumes it is apparent to most readers that Doug's "...all
on Earth..." refers actuality's portion which is massive:
fermionic (spin 1/2) and posentropic. This is what inept classical
hylics
deludedly refer 'state-ic, immutable, objective, material, substantial,
formal, mechanical reality.' Adepts grasp that photons (bosons,
spin 1, integerentropic, etc.) may travel much faster and explicate
much of quantum~evolution's transmutative
processing on Earth. Allow Doug to use quantonic script to show
quantons for both
entropa and
cohera:
both quanton(mixentropa,quanton(negentropa,quanton(zeroentropa,posentropa))),
and quanton(mixcohera,quanton(isocohera,quanton(cohera,decohera))).
Allow Doug to show latter in terms of quantum flux spin nomenclatura:
quanton(mixspin,quanton(isospin,quanton(integer_spin,fractional_spin))).
In terms of adiabaticity we can script quanton(mixadiabatic,quanton(isoadiabatic,quanton(adiabatic,n¤n_adiabatic))).
An exotic exemplar of mixing
in real quantized timings is a neutrino which quarter cycloidal~cycle
alternates self-spins of (iso)integer and fractional. This facilitates
one of quantum reality's great miracles of a partial
fermion (neutrino as quanton(boson,fermion)) penetrating enormous
masses and mass densities at near light speeds without apparent
self-other 'damage.' Of course that is 'motion.' However, it
isn't in cosmic cycloidal motion 'class' which Doug is using
relevant equilibrium here. We should, though, be capable
of describing other classes of 'motion' using quantiques autsimilar
those desnoured here. Doug - 21Feb2012.
28Jun2012 Begin Spatio~Temporal Folding Aside:
In that prior paragraph Doug introduced quantum~memeos of
"...other classes of 'motion.'" Specifically, neutrino
motion as plausibly n¤n cycloidal.
Ever watch that fab flick Dune?
(For Doug) Its most intriguing exegesis is teleportation as a
quantum~phenomenon: "...folding time and space."
Doug would ask adepts to read that as "...foldings of timings
and spacings." Latter is a more holographic complementarospective.
Too it offers quantum~stage
isohologra[[il][m][ph]]icityings of Hugh Everett's multiverse(ings).
We can even make inferences re Bohm's enfoldment, specifically,
exposed in one of many ways ostensibly~potentially as, "neutrino
n¤n cycloidal motion."
We know neutrinos are real. We can imagine quantons
similar neutrinos which aren't limited to light speed.
Catastrophe theory needs some quantum~memeos autsimilar these
to offer heuristic actual views of space(ings) and time(ings)
foldings.
Now stretch your quantum~stage noodlings!
What
are implications of quantum~enfoldings~unfoldings nissin quantons(chaos,equilibria)?
Chaos theory come to mind? Butterfly affectings? Quantum~partiality
of chaos in equilibria and equilibria in chaos? What about rqcsings of those partialityings?
If I were a young person and wanted to choose an area for
my life's opus, this just might be it. It has much to do with
cosmic subjects, but biology and medicine too: equilibrium
as potential health (also tentative remission), chaos as change
into quantons(better,worse) health, etc.
Doug - 28Jun2012.
28Jun2012 End Spatio~Temporal Folding Aside.
As you may choose to surmise then, no 'anything' can be said
to have "zero momentum," period. Too, no anything can
ever return to its 'original locus.' Further, all 'anythingings'
are self~other~evolving at up to Planck rates.
That implies, at least to Doug, that reality in general is
absolute change. Change borne of absolute quantum~flux. A great
quantum~miracle is that quantum~flux may be viewed stochastically:
uncertainty
reigns and chance
reigns. Being stochastic, though, implies that chance and uncertainty
aren't absolute: their frequencies,
changes, and gradients near to
and far from equilibrium are quantum~guessable.
"But Doug, what about reversibility?"
In general, absolute movement~motion cannot be 'reversed.'
Most processes cannot be reversed! Earth can never 'return' to
where it was. Ditto Milky-Way. Ditto galactic clusters. Classical
reversibility is an apparition. We can never 'reestablish initial
conditions,' especially cartesian locus. Our comtexts
are always changing, perpetually evolving,
absolutely.
'Stability' is a wet dream of Keynesian, Marxian, Socialist,
and classically retarded hylic
minds.
Clearly then, a huge issue in omniscussing classical vav quantum~equilibria
is that we must no longer view classical-equilibrium as 'state.'
We must adapt quantumly to viewing equilibria as absolute 'change.'
Those are two cosmic views vastly omniffering one another.
More to come...
Begin 14Sep2012 Extended Omniscussion
on Reversibility Aside:
Following Doug's approach just above
(under cycloid graphic) on spin, cohera, entropa, and adiabaticity,
allow Doug to write a similar script for reversibility. In terms
of reversibility we can script:
quanton(mixreversibility,quanton(isoreversibility,quanton(reversible,n¤n_reversible))).
Philosophical, metaphysical, scientific,
physical, logical, and pneumatic implications of that script (combined with
others above) are enormous.
Permit Doug to repeat his 'in general'
summary, "In general, absolute movement~motion cannot be
'reversed.' Most processes cannot be reversed! Earth can never
'return' to where it was. And so on..."
I wish you share Doug's dawningq
here. Reversibility HotMeme™ "Reversibility
and its partial quantum~complement n¤n(un)reversibility
mimic certainty and its partial quantum~complement uncertainty."™ Reversibility HotMeme™.
Quantum~reversibility issi quantum~uncertain.
Why? Quantum~absolute change, as n¤nabsolute-stochastic
quantum~unreversibility mimicking n¤nabsolute-stochastic
quantum~uncertainty.
Compare classical repeatability...nowings.
Then compare classical canonic OSFA 'definitions' of verifiability,
analyticity, formality, mechanicity, truth, proof, scalar measurement,
state, stability, concrete, stoppability, equilibria,
chaos. List is endless...
Doug has said, "Digital is dead."
Why? Digital is 'certain,' formal, mechanical, analytic, objective,
reversible, repeatable, etc. Doug also claims, "Classical
maths are dead." What shall we do? Quantum~computing and
quantum maths.
Quantum~reality is perpetually and ubiquitously
hologra[[il][m][ph]]ic, alive, aware, con(m)scious, and forever
evolving, changing...the account, the logos.
Heraclitus re the account,
- "On this account which
holds forever men prove uncomprehending, both before hearing
it and when first they have heard it. [B 1] (Diels Kranz B-Texts),
and
- "For that reason you must follow
what is common. But although the account is common, most men
live as though they had an understanding of their own. [B 2]
(Diels Kranz B-Texts)."
Doug ciphered Heraclitus' B2 using Bergson
and Suares like this,
- "For that reason you must follow
semasiologies of cosmic energy, cosmic flux. But although
the account is one of cosmic flux, most men live as though
they had a dialectical state-ic interpretation of their
own."
In general, and this is Doug's linguistic
condensation here, chaos, equilibria, and their gradiencings are quantum~uncertain, and quantum~n¤n~reversible.
Doug.
End 14Sep2012 Extended Omniscussion
on Reversibility Aside.
Doug - 26Jul2011.
End a Doug 26Jul2011 Equilibrium vav Reversibility Aside.
Now we know...classical notions of 'state' as equilibrium
are a totally bogus way of thing-king about reality. It
is contrived, convenient, provincial, parochial,
patriarchal, polemic, proscriptive ("thou shalt 'nots'..."
spewing forth abundantly), unitemporal, bivalent (essence of
classical opposition and contradiction), and literally
unwise...it is classical
binary, either-or dialectical stupidity at its most glaring manifestation
of Error.
Classical notions of 'equilibrium'
are just plain bogus.
All of classical 'science' is like that, however. That
must change! It is imperative to change it and to remediate it.
To do so, Doug has to invoke some quantum~n¤nmechanical
assumptions. Two big assumptions are that:
- quantum~reality is absolute change born of absolute flux
as its core memeo
of reality, and that
- all change involves heterotemporal
and heterostochastic quantized
quantum~phase~encodings
of all absolutely changing flux.
Omniqueness(ings) emerge(s) here (thus denying classical notions
of, for example, 'identity') which declares all phase~encodings
complementarily omniffer (a way of saying,
"ubiquitous and perpetual many to many quantum~holographic~antinomialism
- Doug - 5Dec2014) all other phase~encodings in
quantum~reality.
Autsimilarity
'exists,' but there are n¤ identities
in quantum~reality!
So Doug's challenge here is to remediate static and objective
classical 'equilibrium' notions with stindyanic
and quantonic quantum~equilibrium memeos.
Now, reader, please realize how 'equilibrium' of 'state' appears
simple.
Comparatively, and these are wholly novel memes we are encountering,
æquihlihbria
of absolute change
may appear complex. There are enormous challenges here. That
means our efforts will be incomplete, i.e., quantumly~partial.
We only need rudiments of omniscrimination
twixt classical and quantum, however. Doug can do that!
Begin a Doug
16Jul2011 Equilibrium vav Stability Aside:
Classically, equilibrium and 'state' are close kin. Classical
equilibrium is Keynesian 'stable,' it holds still and One Equilibrium
Fits All (OEFA). Worse, classicists assume that Keynesian 'stability'
can be controlled (TQC
of a fiscal sort) and planned-made perpetually stable. If you
grasp essentials of quantum~reality you also fathom how incredibly
retarded a notion of Keynesian 'stability' is.
This is a core issue of Quantonics' position on FEP
equilibria notions (classical) and memeos (quantum), and
how perpetually evolving quantum equilibria are hyper
a classical notion of Keynesian 'planned' and perpetually static-stable,
ideally status quo, OEFA equilibrium.
Doug can make this more clear and apparently easy to grasp
using two bullets:
- Keynesian classical 'equilibrium' is 'planned,' 'ideal,'
and perpetually stable, vis-à-vis
- Quantonics' quantum equilibria are tentative and perpetually
evolving from one (previous) equilibrium to another evolved and
newer one.
If you concur with those con(m)clusions by Doug, then you
may grasp how impossible it is for Keynesians to achieve FEP
'stability' using 'planning.' Classical dialectical
'reality' is a ruse, a 'ç a t h o l i ç' (universal)
'equilibrium' Keynesian Ponzi
of unbelievable proportions. See wikipedia on Ponzi.
Hayek and von Mises have warned us about this. Their warnings
are about to bear actualization, and most of us (alive today)
are fortunate enough to be living in a time of huge change from
an old and worn Keynesian equilibrium to many n¤væl~but~only~tentative
and quantum~ensemble of vicissitudinal
evolving quantum equilibria.
More narrative imminent here during next week or two...
End a Doug 16Jul2011 Equilibrium vav Stability Aside.
. . . 25-30Mar2011...
Doug is using Prigogine's
and Stengers' (P&S') text titled Order Out of Chaos,
Bantam, paperback, 1984 as a reference for most of his work here.
Their opus now, in that text's regard is over 27 years ancient.
They are classical mechanics broaching quasi~quantum memeos using
dialectic's problematic French (translated from their native
tongues) and English languages. Their work needs quantum~remediation,
in Doug's opinion. However, their minds are superb and Doug wants
to extend their opus in areas surrounding memes and memeos of
'equilibrium,' both classical and quantum. As a result, Doug
finds it valuable to review that text in parallel with his efforts
here and in his own new textbook. It will slow us down, but long
term results will be extremely valuable and inimitable as quantonics'
novelty. Far From Equilibrium, FFE-work in and of itself. Apropos!
To assist Doug's efficiency, he wants to introduce some new
intra quantonics acronyms: FFE (Far From Equilibrium),
NTE (Near To Equilibrium), and SAE (Stoppability AKA Atemporality
At Equilibrium). We need to omniscuss
FFE and NTE both classically and quantumly. Just now it appears
to Doug that SAE only applies in classical contexts.
P&S' opus associates many other memes with 'equilibrium.'
A key meme is one of reversibility. Their version of reversibility
is classical. Their view of time is classical too. Time to them
is a monism: One Time Fits All (OTFA). Their non classical
notions and ideas are yet unitemporal. But for them that
is a big leap forward since they claim that classical hard 'science'
is actually atemporal:
Doug calls this "stoppability." (This is a large part
of Einstein's total failure in his construction of mechanical
Special- and General-Relativity Theories.) They also claim that
soft sciences have made most progress in temporal views of reality,
so in that sense they are far ahead of hard science itself. Of
course hard sciences simply do not 'work' (are not viable) without
assumptions of atemporality and stoppability. Their laws
and analytic (i.e., formal decomposition) tools fail when applied
to quantum~evolving
systems! P&S refer Henri Louis Bergson, however, they
miss what Mae-wan Ho observed: Bergson's metaphysics
calls for heterotemporalityings.
That's quantum! See Doug's review of Bergson's Creative
Evolution.
If equilibrium is omnifficult to explain...well, I'm unsure
whether explaining 'reversibility' is as omnifficult, perhaps
more, perhaps less so. Doug has done a QELR of 'reversibility,'
but it is inadequate for issues which arise here. Since these
two memes are so 'intertwined' with one another, Doug senses
he should keep them together here until most unsaids have been
desnoured to our own satisfaction.
P&S only speak of unitime as ideally reversible near classical
equilibrium. They claim that unitemporal irreversibility (again,
classical) only appears under FFE contexts. Most of their
reasoning is spawn of classical thermodynamic theories. Classical
thermodynamics assume unitime and single gradient posentropy,
i.e. an arrow of time which inevitably carries actuality to an
imminent and certain 'heat death.' In their text, though, they
well convince readers that posentropy has two gradients:
a 'negative' one which generates actuality itself, and a 'positive'
one which conservatively degenerates ('reverses') actuality
back to ultimate chaos. Issues born of these last five or so
paragraphs are horrendous.
You may recall that Pirsig used a notion of 'latching.' See Doug's recent CeodE October,
2012 QELR of 'latch.' Reality's creative evolution, to Pirsig,
latched novelty. We may choose to see latching as irreversibility.
And for this local work effort, it simply explains what P&S
are calling 'irreversibility.' We can hermeneut this in agreement
by saying, "Novel creation AKA latching occurs
at FFE." Placing that in currency's lime light, "Death
of Keynesianism is a FFE process of countless ensemble affectings."
And that is happening now as we watch! Doug - 30Mar2011.
Allow Doug to start a list of issues for further omniscussion
(Doug is showing main issues first, then will go more specific
on reversibility vis-à-vis irreversibility next):
- State vis-à-vis flux,
- Basic classical theory assumes 'state.'
- This has immense bogus (low 'value') implications for classical
notions of equilibrium and reversibility (and all other classical
thing-king).
- N¤n mechanical quantum empiritheory
assumes ubiquitous up to Planck rate flux (isonic n¤n~spins,
plus bosonic zero, integer, and fermionic 0.5 spins).
- This puts Value back into all human thinkqing
about reality, including memeos of equilibrium and reversibility.
- Ubiquitous quantum~flux, hyper classical notions of
state, offers many notable implications for classical vis-à-vis
quantum hermeneutics of equilibrium and reversibility.
- Classical reversibility implications:
- Quantum reversibility implications:
- Classical atemporality
implications:
- Quantum atemporality implications:
- Classical equilibrium implications:
- Quantum equilibrium implications:
- Certainty vis-à-vis uncertainty (see Doug's quantum
vis-à-vis classical measurement),
- Basic classical mechanical theory assumes ubiquitous certainty.
- Basic classical mechanical quantum theory assumes microscopic
uncertainty and macroscopic classical certainty.
- N¤n classical quantum~empiritheory assumes EIMA
holographic Ensemble~Quantum~Uncertainty (EQU):
quantum~uncertainty reigns
all scales of quantum~reality.
- Ubiquitous quantum~uncertainty, hyper classical notions
of certainty, offers many notable implications for classical
vis-à-vis quantum hermeneutics of equilibrium and reversibility.
- Classical reversibility implications:
- Quantum reversibility implications:
- Classical atemporality implications:
- Quantum atemporality implications:
- Classical equilibrium implications:
- Quantum equilibrium implications:
- Monism vis-à-vis pluralism,
- Classical continuous 'state' informs and immanates all
monistic classical thought with dialectical bivalency.
- Quantum~flux, with up to Planck rate complementary quantization,
emerqs, pluralizes, and holografies all heterogeneous
quantum~thinkqing with quantonic~omnivalencyings.
- Ubiquitous quantum~pluralism, hyper classical notions
of monism, offers many notable implications for classical vis-à-vis
quantum hermeneutics of equilibrium and reversibility.
- Classical reversibility implications:
- Quantum reversibility implications:
- Classical atemporality implications:
- Quantum atemporality implications:
- Classical equilibrium implications:
- Quantum equilibrium implications:
- Classes of time,
- classical time as temporal monism, time as homogeneous, ideal
absence of quantization, Planck's clock intentionally turned
off, etc.
- quantum~time
as radical and stochastic quantized~timings as spawn of quantum
flux enabled by Plancks clock's perpetual ticking
- Ubiquitous quantum~timings, hyper classical notions
of monistic time, offer many notable implications for classical
vis-à-vis quantum hermeneutics of equilibrium and reversibility.
- Classical reversibility implications:
- Quantum reversibility implications:
- Classical atemporality implications:
- Quantum atemporality implications:
- Classical equilibrium implications:
- Quantum equilibrium implications:
- quantization of time (all flux is quantized so then too are
mass, space, and gravity, etc.)
- etc.
- What about phase?,
- quantum~phase~interrelationshipings are quintessence of all
quantum~evolution, thus all emergent quantum~creation and novelty
- spontaneous (free will; n¤n inert) phase~interrelationshipings
depend intrinsically upon massively plural and ensemble
quantization of all quantum~flux
- gravityings now may be viewed as one quantum~stochastic~holographic
kind of quantum~phase~interrelationshipings
- massings now may be viewed as one quantum~stochastic~holographic
kind of quantum~phase~interrelationshipings
- spacings now may be viewed as one quantum~stochastic~holographic
kind of quantum~phase~interrelationshipings
- timings now may be viewed as one quantum~stochastic~holographic
kind of quantum~phase~interrelationshipings
- entanglement
and its partial presence~absence is key to quantum~scintillation's
creative changings, e.g., Higgs boson and creatio ex nihilo
aperio and QED and QCD
- classical absence of quantization leaves all flux unquantized
(as closed, static-tautological transverse y=f(t) classical sinus
flux) and Bergsonian 'inert,' not spontaneous (absence of free
will: causally determinate; ideal absence of quantum~chance and ~uncertainty)
- Ubiquitous quantum~phase~quantization, hyper classical
notions of scalar phase, offers many notable implications for
classical vis-à-vis quantum hermeneutics of equilibrium
and reversibility.
- Classical reversibility implications:
- Quantum reversibility implications:
- Classical atemporality implications:
- Quantum atemporality implications:
- Classical equilibrium implications:
- Quantum equilibrium implications:
- etc.
- Thermodynamics,
- As Doug has vociferously explained in Quantonics, classical
thermodynamics theories are mostly and simply bogus:
- single class of entropy: posentropy
- assumes a single degenerative gradient to posentropy
- entropy as a static scalar classical dialectical concept
- assumption of classical 2nd 'law' as general to
all reality (it is only partially specific to material, posentropic
reality)
- assumes conservation and closure of universality
- assumes that mathematics are adequate to describe entropy
- assumes that English, French, German, and other dialectical
languages systems are adequate to describe entropy
- etc.
- Analyticity,
- Positive,
- Negative,
- Entropa,
- Cohera,
- Conservation,
- Closure,
- Scalars of measurables,
- Newton's atemporality
as a primrose lane,
- Etc.
Doug - 24-30Mar2011.
Chapter 2 Review Summary of P&S' Order Out of Chaos
- 1Apr2011 - Doug:
Classical dynamics theory is based in Galileo and Newton,
plus a few others' classical notions. That is essence of what
P&S narrate in Chapter 2.
Doug's assessment re: classical dynamics is...that
is what current Keynesian thought uses. So we can express a strong
opinion that Keynesianism is doomed. At this juncture that opine
is essentially cliché, and Doug acknowledges such. What
is important is that we cannot use classical dynamics notions
to extract valid memes of real equilibrium. We have to move past-passed
classical dynamics in order to provide a Quantonics QELR of 'equilibrium'
which is at least potentially more valid than what most currently
use now.
"Doug, what's wrong with classical dynamics?" Doug's
list should seem familiar, and it emerges from his draft review
of Chapter 2 of OOoC:
- objectivity,
- stoppability,
- lisrability,
- quantity,
- negation implying unitemporal reversibility (more important
here, though, is an intrinsic that quantum~reality is only positive),
- predication,
- unitemporality implying continuous y=f(t) (big issue with
Keynesianism),
- time as homogeneous delta-space/space proxy (no valid 'concept,'
no valid understanding of time),
- change as temporal 'motion,' (no valid 'concept,' no valid
understanding of change),
- static 'completeness' as easily achievable and assessable
under canonic classical dynamics theory,
- closure,
- conservation,
- commutability, commutativity,
- equivalence- and other -relations, (i.e., identity, reflexivity,
symmetry, inequalities, associativity, distributivity, normative
assignment, signification, etc., re: classical identities 'should
be' 'classically Aristotelian-tautologously' 'reversible-commutative,'
but they are n¤t due quantum reality's real and absolute
change)
- etc.
Classical dynamics canonically assumes all of those. Many
of those list items involve even other implicit assumptions too.
What is crucial to grasp is that Quantonically and quantumly
all of those are "simply and demonstrably bogus."
'Modern Keynesianism' assumes all of those and more. Keynesianism
is bogus! Indubitably, Keynesianism is bogus. We may say then,
Keynesianism is in its death throes as Doug writes this. It is
only a matter of timings.
"Doug, can you list quantum~memeotic complementaries
of those classical notions?" Yes, but we must not treat
them as classically bivalent 'opposites:'
- subjectivity,
- absolute change, perpetual change, plural changings,
- holographicity, middle~inclusion, everywhereings~everywhenings~associativityings,
- quality,
- cancellation of positive only fluxings,
- evolution,
- perpetual and ubiquitous quantization of all reality,
- all quanta and all of their ensembles have their own local~n¤nlocal
omnique massively heterogeneous timings,
- all quanta and all of their ensembles have their own local~n¤nlocal
omnique massively heterogeneous omnivalently evolving changings,
- any quantum~assessment
of systemic
completeness is always quantum~partial, Links added 10Mar2012
- Doug.
- perpetual and ubiquitous openness,
- quantum~reality's potentia are unbounded,
- autsimilarity of quantum~EWings,
- autsimilarity of EWings' EIMAssociativityings,
- etc.
Neither of those lists is even close to being 'complete,'
and they likely never will be. What we have though are
lists which can be compared in our assessments of valid views
of a more innovative approach to systemic equilibrium and transitions
among equilibrial quantum~modalityings.
This 1Apr2011 narrative of OOoC's Chapter 2 is only
intended as a brief summary of classical vis-à-vis quantum
dynamics' comparative issues.
End Chapter 2 Review Summary of OOoChaos - 1Apr2011
- Doug.
. . .
Chapter 3 Review Summary of P&S' Order Out of Chaos
- 5Apr2011 - Doug:
P&S' OOoC Chapter 3 is a kind of brief history
of people of interest who participated in 'developing' classical
dynamics theory. Included as transitionals from classical to
quantum dynamics are a select few others.
This chapter is a blunt indictment of classical science. It
repeatedly narrates importance of ditching classical science
and moving on to something better: a whole new way of
thinking about non classical dynamics. P&S appear to miss
classicists' core satan of classical dynamics:
dialectic. However, they narrate much of what falls in a category
of 'dialectical thing-king' as what is wrong with classical dynamics.
They do us a great service! They name names. Those most in error
include:
- Kant (a dialectician; Kant bivalently split Subject and Object,
noumenal and phenomenal, philosophy and science...Kant is an
epic failure: "scientific choice is heresy"),
- Hegel (a dialectician),
- Diderot (though Doug would put him in both lists, for a variety
of reasons),
- Descartes (a dialectician),
- Newton (a materialist dialectician mechanist),
- Lagrange,
- Hamilton,
- Duhem,
- Poincaré,
- Kirchoff,
- Mach (minimalism as economy of thought),
- Plus positivists, in general, e.g., Reichenbach (mathematical
physics as a last resort of understanding time and reality and
denial of nature as our partner since man is above god, rather
"there is no god," and man is above nature...this is
simply incompetent humanism gone awry, gone amok...),
- etc.
These 'people' shared a common flaw in their thing-king: "Preserve
science at all costs. Control nature using 'science.' Humans
are above nature and god."
Doug loves Prigogine and Stengers mostly since they defy and
deny said views for what they really are: intrinsically flawed.
They challenge classical science as essentially bogus, and they
narrate how classical 'science' is mostly just humanly-convenient
lies. Doug agrees both in spirit and belief. It may be clear
to readers that this old human 'mindset' is an agent of those
classical humans' imminent self-extinction.
Comparatively we may juxtapose a few transitionals, those
commencing a quantum~journey:
- Bergson (he understands vast problematics of classical science,
he understands: the
account, AKA the logos, and he appears to say "one
must find one's inner
before one can even begin to understand nature;" Bergson
somewhat like James appears as a gnostic; for Doug that is a
prerequisite for grasping a modal of reality as quantum~holographic),
- Stahl (Doug lacks familiarity with Stahl),
- Whitehead (essentially process as natural which is implicitly
quantum if we view all processings as quantized),
- Diderot (he straddled classical and quantum which puts him
in both camps, for a variety of reasons...)
- Plus all quantumists (non dialectical ones) whom Doug attempts
to uncloak in Quantonics (most of these, like Diderot, tend to
straddle(new_quantum,old_classical) so it isn't trivial to assess
them as pure...we may, only as a reference, consider Quantonics,
Gnosis, the logos, and Autiot as nearer 'purety'),
- etc.
I highly recommend OOoC as Quantonics student "must reading."
Read it over and over and over until you commence grasping much
deeper issues here.
End Chapter 3 Review Summary of OOoChaos - 5Apr2011
- Doug.
. . .
10,12-13April2011: Begin - A comment on classical vis-à-vis
quantum 'reasoning.'
I do n¤t enjoy saying this, but I feel have n¤
alternative...it must be said. In Doug's opinion, anyone who
thingks we can use
classical logic to
understand economics and equilibrium (in terms of inflation,
deflation, and hyperinflation) is just plain retarded.
Just to set our tone and tenor for what follows...
Prior Doug's continuing his review of Chapter 4 of OOoChaos,
he wants to offer some novel memeos regarding classical 'logic'
vis-à-vis quantum coquecigrues.
If you read current pundits' descriptions of inflation vis-à-vis
deflation and hyperinflation, you will hear them talking and
writing about those comparisons using logic, using rational reason.
Doug wants to reiterate: we will never understand inflation
vis-à-vis deflation and hyperinflation as long as we continue
using classical models of reality and classical logic to describe
them. Regardless what Lira and Ferguson say, classical dialectical
logic and reason are simply bogus. They are bogus to their very
core. Dialectical and dialethic logics are demonstrably bogus
when we leave SOM's Box and enter
quantum~reality.
Doug has another new graphic to help explain why. He calls
it, "Equilibria (Equilibrium) as Many Interrelationshipings."
All equilibria are quantum~ephemeral. Their comtextings
are multiplicate, quantized
and evolving. Let's take a look:
"Evanescent neural organizations take place as each neural aggregate recodes
its input[s]."
Karl Pribram in his languages of the brain, Prentice-Hall,
1971.
See Chapter 4, p. 82 'synopsis.'
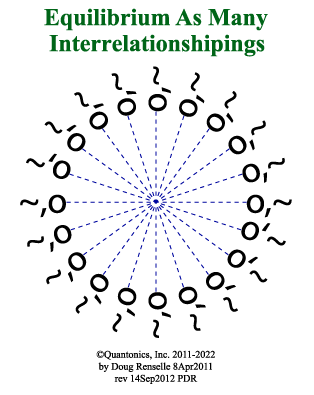 |
Details of that graphic need more description here.
Circular shaped portion represents 'equilibrium' as
an energy~wellings.
Essentially it is a 'nest,' a
network of interrelationshipings.
Those interrelationshipings appear as
o,~  quanton(o,~)
also quantized as this:
¤,~ quanton(o,~)
also quantized as this:
¤,~  quanton(¤,~)
So EWings
are networks of interrelationshipings each of which may be a
network of interrelationshipings.
'Quantum logic,' thus has to ¤mnit¤r
energy~wellings' networks of interrelationshipings. quanton(¤,~)
So EWings
are networks of interrelationshipings each of which may be a
network of interrelationshipings.
'Quantum logic,' thus has to ¤mnit¤r
energy~wellings' networks of interrelationshipings.
N¤ classical bivalent 'logic' can do this, period, which
is why Doug
calls classical logics' pundits "retarded." To claim
that classical logic can is to declare
oneself, literally,"a moron." I.e., "I...said
classical logician...am a moron!"
We may choose to see ad
occulos that quantum~coquecigrues is a
n¤n dialectical 'logic' of quantum~scintillating
dynamic~evolving network interrelationshipings.
We may choose to squeeze essence here as quantum~omnivalence
vis-à-vis classical-bivalence.
However, it isn't that simple. More squeezing juices quantum~spontaneity
vis-à-vis classical-state.
Again, more squeezing extracts quantum~quantization vis-à-vis
classical linear continuous thing-king.
And so on...
Ferguson and Lira use classical logic's static bivalence
to 'reason.'
Their versions of inflation, deflation, and hyperinflation are
impotent.
Quantum~gn¤stics use evolutionary~omnivalencings
to understand.
Thæir quantum~versions of
inflation, deflation, and hyperinflation are p¤tænt.
Pick up on this at 12Apr2011...
Regular readers know that Doug compares Quantonics
to Autiot frequently.
Why?
A quantum~feature of Autiot is holographic cosmic~energy self~other
fractal recursion.
Doug uses an acronym for that: sorso. Sorso means "self~other
referent sophism."
That is what quantum~holograms do.
Any 'logic' applied to any sorso reality must be a 'quantum logic.'
Classical logic doesn't assume sorso. Coquecigrues
assumes and presumes sorso.
Quantum~reality has many non classically logical 'features,'
including:
- sophism,
- self~reference,
- other~reference,
- fractal recursion,
- quantization,
- choice(ings)~chance(ings)~change(ings)~spontaneity,
thence,
- scintillation, thence,
- evolution,
- every~H5Wings~included~middlings~associativityings,
- holographicityings,
- Balmer Ladder ensemble EWings' networkings interrelationshipings
(full quantum spectral coverage),
- etc.
|
Classical dialectical logic cann¤t apply its
invalid 'reason' to those quantum~realisms,
without imposing anti~quantum classical 'state,' independence,'
'objective negation,' etc.
I have a lot more to say here. I will work on this
most of next week...
Doug - 10,12-13Apr2011.
10,12-13April2011: End - A comment on classical vis-à-vis
quantum 'reasoning.'
. . .
15-16April2011:
Begin - A comment on classical vis-à-vis quantum 'gradience.'
Doug had another of those immense epiphanies last evening.
Allow me to attempt a reconstruction of events...
I had just finished my evening snack of ripe olives, cattiatore,
and mozzarella with champagne. I decided to restart my rereading
of Chapter 4 of P&S' OOoC. This is about my third
possibly fourth pass at this chapter. My epiphany arose when
I read this:
"...As for the birth of the 'science
of complexity,' we propose to date it in 1811, the year Baron
Jean-Joseph Fourier, the
prefect of Isère, won the
prize of the French Academy
of Sciences for his mathematical
description of the [mechanical,
formal, analytic] propagation of [classical] heat in [classical]
solids.
"The result stated
by Fourier was surprisingly simple and elegant: heat flow is proportional to the gradient
of temperature. It is remarkable that this simple
law applies to matter, whether
its state is solid, liquid,
or gaseous. Moreover, it remains valid whatever the
chemical composition of the
body is, whether it is iron
or gold. It is only the coefficient of proportionality between heat flow and gradient
of temperature
that is specific to each substance.
"Obviously, the universal character of Fourier's
law is not
directly related to [classically] dynamic interactions as expressed
by Newton's law, and its formulation may thus be considered
the starting
point of a new type of science. Indeed, the
simplicity of Fourier's mathematical
description of heat propagation stands in sharp contrast
to the complexity of matter
considered from a molecular
point of view..."
Transcribed from p. 104, Chapter 4, OOoC by Doug. Doug's
brackets. Doug's bold violet [classical problematics] and green
[quantum precursors] highlights.
In spite of its bold violet objective dialectics this segment
of text is prescient, to say a least. Prescience is available
to us, at a very least, in dark green bold text Doug highlighted.
A key surmise by P&S in that text which might easily be
overlooked is their claim of "simplicity." Our nexus
here is Bergson's, paraphrased by Doug, "...state is complex
and flux is simple, since state cannot explain flux but flux
can explain state." We see Bergson's implicit claim that
exegesis is a hallmark of simplicity in terms of one's being
enabled to understand.
That nexus becomes a fulcrum for Doug's epiphany!
Do you recall Doug's more than a decade-old epiphany which
he described in his web page titled, Have
a DQ Moment?
Essence of that page is this: mass, length (space),
and time as plural participling quantons are all quantum manifestations
of quantum~flux!
If that is so, What about temperature, and temperature gradience?
Yes, temperature and its gradients as plural participling quantons
are all quantum manifestations of quantum~flux! All measureables
(ømnihtørables
in quantumese) as plural participling quantons are all quantum
manifestations of quantum~flux!
Flux simplicity, as Bergson instructed, rears itself and sparkles
in its majesty over (hyper) classical 'state.'
"What is such a big deal here, Doug?" P&S describe
all physical measurables above as 'classical scalars:'
temperature, heat flow, gradience, etc. They describe classical
dynamics as an event-state
ontology. Fourier did too. Why? That is what mathematics do!
Bergson instructed us well on that issue too. Ditto Keynesianism.
Ditto Ferguson and Lira's classical 'logic' and 'reason.' Ditto
all classical 'economics pundits.' Ditto classical notions
of equilibrium and reversibility.
Implications of what Doug has written in this 'gradience commentary'
are astonishing! Doug will spend several days here showing you
that.
16Apr2011...continue...
In our quotes from beginning of Chapter 4 above, P&S (like
all classicists) treat physical measurables conventionally as
scalars and at best as Newtonian formal motion of stoppable (atemporal) 'state-events.'
Allow Doug to requote those bold green text segments and cipher
them both classically and quantumly:
- classical heat flow ciphers:
- "...classical scalar heat flow is scalar-proportional to the
scalar gradient
of scalar temperature..."
- "...the classical scalar coefficient
of classical scalar proportionality between scalar
heat flow
and scalar gradient
of scalar
temperature
that is specific to each substance..."
- "...the starting point of a new type of science..."
- quantum heat flow ciphers:
- "...quantum~evolving heat as flux flow is quantum~relatively~phasemental to fluxing
gradientings of temperaturings as flux..."
- "...flux phasemental relativityings
among heat
as flux
flow and gradient of temperature as
flux that is specific to each energy wellings' ephemeral fluxings comtextings..."
- "...the starting point of a new type of quantum~flux thinkqing..."
Yes reader,
"There is a new philosophy in town." Quantum~philosophy
hyper classical-philosophy.
Doug's essence here is that classical thought and language
always ciphers reality as 'scalar state.' However, quantum~thinkqing
always ciphers reality as fluxings' interrelationshipings. As
Bergson wrote, in Dougese, "flux hyper state."
Recently, CeodE 2015, Doug
has been writing a white paper regarding What is Consciousness?
In it Doug used a Fourier approach to describing flow of thought
as quantized processings. He derived his memeset there from his
prior work here. It seems Valuable now to Doug to revisit his
work here and con(m)temporize it analogously from describing
only classical vav quantum 'heat flow' to omniscribing classical
vav quantum 'thought flow' as essence of What
is Consciousness?
30Mar2015 - Begin Aside Comparing Heatc
and Heatq Flow to Thoughtc and Th~oughtq
Flow:
Allow Doug to repeat, to reuse bullet
lists just above and evolve them from memes of heat into memes
of con(m)scious thought:
- classical thought flow ciphers:
- "...classical scalar thoughtc flow
is scalar-proportional
to the scalar gradient
of scalar thingking..."
- "...the classical scalar coefficient
of classical scalar proportionality between scalar
thoughtc flow and scalar gradient of scalar thingking that is specific to each substance..."
- "...the starting point of a new type of science..."
- quantum th~ought flow ciphers:
- "...quantum~evolving th~oughtq
as flux
flow is quantum~relatively~phasemental to fluxing
gradientings of thinkqings as flux..."
- "...flux phasemental relativityings
among th~oughtq as flux flow and gradient
of thinkqings as flux that is
rqcs to each energy
wellings' ephemeral fluxings comtextings..."
- "...the starting point of a new type of quantum~flux thinkqing..."
30Mar2015 - End Aside Comparing Heatc
and Heatq Flow to Thoughtc and Th~oughtq
Flow.
If we apply that to Economics Theory, "Equilibria as
flux is hyper equilibrium as state." Doug believes
we may then bootstrap "flux hyper state" to
most aspects of economic theory. For example, "Reversibility
as flux is hyper reversibility as state." And "Inflation,
Deflation, and Hyperinflation as fluxings are hyper inflation,
deflation, and hyperinflation as states."
More essence
here is that, Quantonics
HotMeme™ "All changes in Value, in quantum~reality, may
be assessed using quantum~gradience of energy~welling
ensembles of quantum~fluxings' interrelationshipings."™
Quantonics HotMeme™.
Energy~welling ensembles link added - 10Mar2012 - Doug. That
link is crucial to eidetically, ad
occulos understanding aspects of quantum~equilibrium being
described here.
Valueq issi gradience(EWingsx,EWingsz)
gradience issi quanton(fluxings1,fluxingsN)
Notice that quantum~gradience is an evolutionary rqcs Value assessment
process
ømnihtøring evolving interrelationshipings among
evolving~energy~wellings.
We may
view changes in quantum
equilibria, then, as evolving rqcs
changings in evolving Value. Quantum~Value evolves.
Equilibriumq issi gradience(EWingsx,EWingsz)
Add 'rqcs' references above.
Doug - 21Feb2013.
Gradience from left to right: higher to lower energy
gradience.
Gradience from right to left: lower to higher energy
gradience.
Recall: quantum~energy is flux rate...shorter wavelengths
have higher relative energy.
Doug - 14Sep2012.
  |
Classical 'value' seeks state-ic 'stability,' AKA 'state'
as 'absence of evolutionary change,' as 'immutability of forms
except for linear motional-state-event analytics as change in
scalar value.'
'equilibrium' is dichon(static_scalar1,
static_scalar2)
Flux is Value. State is 'value.' Evolving flux Value "middle~includes."
Static immutable 'value' 'middle-excludes.' Quantum coquecigrues
hyper Aristotelian
sillygisms.
This appears a good time to check our 'equilibrium' QELR progress.
What did Doug write at beginning of this QELR? This:
"Classical notions of 'equilibrium' are just plain bogus.
"All of classical 'science' is like that, however. That
must change! It is imperative to change it and to remediate it.
"To do so, Doug has to invoke some quantum~n¤nmechanical
assumptions. Two big assumptions
are that:
- quantum~reality is absolute change born of absolute flux
as its core memeo of reality, and that
- all change involves heterotemporal
and heterostochastic quantized
quantum~phase~encodings of all absolutely changing flux.
"Omniqueness(ings) emerge(s) here (thus denying classical
notions of, for example, 'identity') which declares all
phase~encodings complementarily
omniffer all other phase~encodings
in quantum~reality.
"Autsimilarity
'exists,' but there are n¤ identities in quantum~reality!
"So Doug's challenge here is to remediate static and
objective classical 'equilibrium' notions with stindyanic
and quantonic quantum~equilibrium memeos."
How are we doing? Doug is confident we have a partial QELR
of equilibrium. This 16Apr2011 segment has taken us a long way
toward remediation of classical 'equilibrium' notions.
Doug...
...16Apr2011...end
. . .
20-21,24Apr2011: Begin - Chapter 4's title is 'Energy
and the Industrial Age.' Its subtitle is 'Heat, the Rival of
Gravitation.' Commentary.
Doug ignored said titles when he first started reading P&S'
OOoChaos. It just didn't seem important then. But now
it does!
Why did P&S' use those titles for Chapter 4?
An easy answer is Gravity is Newtonian and also any 'then-new'
theories of heat, entropy, and thermodynamics were 'not' Newtonian.
To a casual reader, that may seem unimportant. However, it is
a tell. P&S declare said 'tell.' A tell of
a new science, perhaps a n¤væl n¤n 'scientific'
way of thinking, a new — perhaps Bohmian — n¤n
mechanical psychic~pneumatic quantum~pragmadigm
emerging in an evolutionary manner. (That is what Doug
believes, and that is H5Wings
Doug sees what is happening k~now~ings.)
Essence here
is crucial to Quantonics' New Way of Thinkqing. Grasping
this isn't so tough if you accept a quantum meme of energy as quantum~flux...and very
key to this...quantum~flux is n¤t
classically mechanical. Newtonian (similar Einsteinian)
thought and theory is classically mechanical. Naïvely Newton
treated energy as mechanical, 'not' quantum. Quantum~flux is
n¤t mechanically 'objective,' rather quantum~flux is n¤n
mechanically quantonic, i.e., quantum. Fourier, similar Balmer,
happened upon one tiny essence of quantum reality. P&S
recognized this happenstance.
- Balmer happened upon quantization
as a wave~flux ladder in 1855, and
- Fourier happened upon heat flow based upon temperature gradience
just prior 1811 (date taken from P&S' OOoC text).
Quantum~flux nissin
ænærgy, n¤n classically mechanical 'energy.'
Very basically said quantum~flux expresses itself as bosons and
fermions. Heat is gradient bosonic flux. Fourier partially 'got'
that. Gravity isn't heat, just like Doug has shown that
gravity
isn't Einsteinian acceleration either. Gravity is co~fermionic
attraction. Note two other omnifferencings twixt heat and gravity.
Gravity is atemporal
and its gradience is atemporal. Heat gradience
flow, similar acceleration due
gravity is temporal and its temperature
gradience is temporal. So, to be more correct, P&S might
have shown their Chapter 4 subtitle as 'Heat, the Rival of Acceleration.'
5Jul2015 rev - Change Heat gradience to
Heat flow. Doug.
But we can generalize more than that. We can say that, Quantonics HotMeme™
"All quantum~omnitorables are gradient
interrelationshipings among various kinds of quantum~fluxings."™
Quantonics HotMeme™.
So 'gradient' as used in this section of our review, is both
temporal and atemporal,
depending. Some aspects of quantum~reality are atemporal. Let's
summarize some quantum~fahcts about
what we have written thus far:
- heat flow is temporal,
- heat (temperature) gradience is temporal,
- acceleration is temporal,
- acceleration gradience is temporal,
- gravity is atemporal (i.e., zero latency 'action at a distance'),
and
- gravity gradience is atemporal.
Notice how classical notions of atemporality imply stoppability,
zero-momentum, state, reference frames, etc. Quantum~atemporality
has to do with memeos of superluminality (zero latency regardless
distance of separation) of communications (quantum~correlation)
at a distance and action (e.g., gravity) at a distance.
Gravity is superluminal, in this case though we say and write,
"atemporal." Heat isn't. So heat isn't a rival of gravitation.
Doug...
...20-21,24Apr2011...end
More...over next several days...Doug.
15-16April2011: End - A comment on classical vis-à-vis
quantum 'gradience.'
. . .
Minor rev's to this section 13Apr2011:
This graphic's title isn't generic enough, but Doug
wants it to show you a step ladder
metaphor of increasing energy levelings which we 'classically
count' as wave number.
Here, Doug is using this graphic relevant Finance,
Economics, and Politics.
However, it is generic all quantum~holographic EWing systems.
So wave number, (energy level) of EWings
in a larger EWing, is quantized, and
thus so is many EWings emerqing
a larger EWing quantized. Quantization scales and we can show
(classically rendered Planck) systemic energy as Es Nih.
Where Es is System Energy, N is essentially
wave number, i is square root of minus one, and h is Planck's
constant.
All energy~wellings in our graphic are fluxing perpetually.
All energy~wellings in our graphic are H5Wings~EIMA their comtextings'
quantum~complementary
EWings.
All EWings in our graphic are H5Wings~coobsfecting
all of their complementary EWings in their comtext.
All EWings in our graphic are selectively
(EWing by EWing) adapting
to their Nih.
Where Es is System Energy, N is essentially
wave number, i is square root of minus one, and h is Planck's
constant.
All energy~wellings in our graphic are fluxing perpetually.
All energy~wellings in our graphic are H5Wings~EIMA their comtextings'
quantum~complementary
EWings.
All EWings in our graphic are H5Wings~coobsfecting
all of their complementary EWings in their comtext.
All EWings in our graphic are selectively
(EWing by EWing) adapting
to their
neighbors and their quantum~complementary comtextings.
Doug labeled each with flux~vavings
of 'flux~wavings.' That is their local energy Value,
itself perpetually
adapting selectively to changes in its local and nonlocal environmentings.
Allow Doug to put all of that into a quantum~equilibrium
hermeneutic set of heuristics:
- quantum~equilibral quiescence emerges when EWings' Valuings
are changing 'minimally,'
- quantum~equilibral 'near equilibrium' emerges when EWings
Valuings are changing 'moderately,'
- 'quantum~equilibral 'far from equilibrium' emerges when EWings
Valuings are changing 'maximally.'
|
We ask you to further imagine Inflation, Deflation,
Hyperinflation, and Hypoinflation
as quantum~EWings (quantons) in their various m¤dæs
of H5Wings~quantum~equilibra.
Graphic and narrative are new 22Mar2011 - Doug. Revisions too on 13Apr2011 - Doug.
Doug's Quantonics QELR
of
Equilibrium
©Quantonics, Inc., 2001-2029
|
| Issue |
Classical Equilibrium Issues |
Doug's Classical-Concision |
Quantum~Equilibrium Issues |
Doug's Quantum~Comcision |
| perpetual state as 'stability' |
state not flux |
|
quantumly there is n¤ne |
|
| perpetual evolving equilibria |
classically no such notion
'exists' |
|
flux n¤t state
flux may n¤t be negated
flux may be canceled
by other ideally out of phase (entangledq)
positive flux
all quantum flux is positive
|
|
| middle-exclusion |
SOM's Wall |
|
quantumly there is n¤ne |
|
| middle~inclusion |
classically no such notion
'exists' |
|
we are ihn iht
and iht issi ihn
us |
|
| linear change |
all classical change is closed
y=f(t) motion

Doug - 2Dec2014.
|
|
quantumly there is n¤ne; all motional change
is at least compound cycloidal, e.g., planets; all planet
systems are ihn their planet's cycloidal
changings |
Doug coined Qycloid as a meme for quantized and thus quantum~n¤nlinear
Quantum~Cycloid.
This meme is useful in making more apparent
cosmic levels of quantization, e.g., galaxies and clusters of
galaxies. A stellar exemplar of macroscopic Qycloidal quantization
is rings of Saturn and Neptune.
Imagine Saturn's rings as macroscopic
quantized wave~functions:

Choose to Value highly what this means
for solving one of classical physics' most profound and worrying
problems: the many body problem. Now we may heretically choose
to m¤dal said problem using ensemble wave~functions and
their absolute change, stochasticq chanceq ontologicalq uncertaintiesq
to fathom said problem's depths.
Doug - 2Dec2014.
|
| quantized change |
classically no such notion
'exists' |
|
All actual quantum reality
change is quantized. |
Smallest quantum of change is a tiny packet of Planck rate
fluxings which we may choose to thinkq about as h~bar
and (h~bar)/2. See Planck
quantum. So all real change occurs
at Planck's frequency and subharmonics of that frequency. There
is a problem, though: it likely isn't classically sinusoidal
transverse flux. Packetization almost assures that. Too it is
absolutely adiabatic: 100% energy efficient. Now, what
is interesting is that superatomic nucleonic ensembles of protons
and neutrons are n¤t adiabatic as ensembles. See quanta.
Also see quantization
as and of free will. See Doug on "instability
issi measurement."
Quantization explains directly reality's edict of volitional
vicissitudinality everywhere, everywhen. This is a quantum~miracle
currently and widely unrecognized.
|
| open |
classically no such notion
'exists' |
|
quantum~reality is open
naught in quantum~reality is classically conserved
n¤r closed
|
|
| closed |
classical reality must canonically conserve
and therefore must assume ideal systemic closure |
|
quantumly there is n¤ closure; islandicity and coherence,
but n¤ closure |
|
| entropy |
classical posentropy is the only entropy and it only has
a single gradient: positive |
|
quantum~entropy is an complex ensemble of memeos; at least
four classes of entropy all evolving at up to Planck rates |
See entropa. |
| far conditions |
far removed from previous classical 'state' |
|
when a quantum~system evolves into a radically n¤væl
system we may call it "far from its former equilibrium"
heart sinus fibrillation is a good exemplar; death is a permanent
far from equilibrium condition;
if defibrillation is possible then heart may (only apparently)
'return' to near normal sinus rhythm 'condition'
|
|
| near conditions |
close to but not at ideal classical 'state' |
|
see above |
|
| quiescent
conditions |
ideal classical state |
|
this is what Doug means by quantum~equilibrium
key here is to realize all evolution evolves both gradually
and n¤t far from its former
quiescence; quiescence though, is subject to evolution which
may not be apparent until it is viewed over long periods of timings;
our hologramic minds do this when we sleep; see Bohm and Pribram,
et al.
Doug - 2Dec2014.
|
Ponder a video of
Earth's evolution over last one to two billion years. Say, approximately,
one frame per 50k years. Evolution would be made apparent, and
you should imagine that as SEP of real quantum~evolution. Doug - 2Dec2014. |
| initial conditions |
classical systems can be reset to initial conditions |
|
quantumly there is n¤ne
fathom quantum~reality as unstoppable and unresetable
|
|
| productive gradience |
classically no such notion
'exists' |
|
all quantum~classes of entropy except classical single gradient
posentropy are productive |
See entropa.
See Doug's fuzzon to
fermion ontology.
See Doug's Gen III Quantum
Reality Loop.
Read Ilya Prigogine and Isabel Stengers' Order Out of Chaos.;
they show that posentropy has two gradients: classically positive
(heat death), and generative.
|
| dissipative gradience |
classical thermodynamics and entropy theory canonically prescribe
posentropy's perpetual dissipation of high entropy systems (systems
which have used up much energy flow and thus entropy in their
'creation') |
|
|
See classical vis-à-vis quantum dissipation. |
| emergence role |
classically no such notion
'exists' |
|
OEDC is real
in quantum~reality |
|
| deemergence role |
systemic death AKA eschaton |
|
OEDC is real in quantum~reality |
|
| energy wells |
mechanical and formal versions only |
|
all EWings in quantum~reality are quantonic |
|
| attraction |
mechanical and formal versions only |
|
quantum~attraction takes many subjective, qualitative, fluxic
guises:
- fermionic,
- bosonic,
- quarkic,
- gluonic,
- coherence,
- gravity,
- similarity,
- selection,
- omniscrimination,
- ontic,
- energy~welling,
- holographic,
- interference,
- entanglement,
- cognition,
- recognition,
- awareness,
- etc.
Doug - 2Dec2014.
|
Compare di-scriminationc and omni~scriminationq
as means of selecting 'attraction.'
See 'discriminate' and its QELR.
Doug - 2Dec2014.
|
| logic |
bivalent either-or only allowed AKA bivalent alternative
denial; ideal paired opposition of all concepts |
|
quantumly there is n¤ne ideally classical |
|
| coquecigrues |
classically no such notion
'exists' except in Voltaire's Gargantua and Pantagruel |
|
quantum~logic is naught at all like classical logic |
See Doug's coquecigrues. |
Doug's Quantonics QELR
of
Equilibrium
©Quantonics, Inc., 2001-2029
|
As you may choose to see, Doug has a huge amount of work here
to lay foundation for understanding equilibrium in systems theories
both from classical and quantum~systems viewpoints.
This is going to take awhile. Please be patient. I want to
finish it, but...more...I want to get it as close to better
as is possible for limited~me to do. We do have some emergent
progress, however!
Doug - 20Mar2011.
Begin 22-24Sep2011 Equilibrium
Update:
An issue of order...
Classical order is stable-state-ic cartesian-locality. This
is reference-frame (contextually-free) referred "classical
physics' absolute 'order.' "
Quantum~¤rdær issi fluxing complementary n¤nl¤cality.
This is comtextually dependent quantized~¤rdær.
It is dynamic, evolving order borne of two quantum miracles:
quantization and scintillation at up to Planck rates.
Doug has been reviewing selected texts from his private library
for index references to 'equilibrium.' Doug's first choice under
Bohm is his and B. J. Hiley's The Undivided Universe.
Doug could find no index item for 'equilibrium.' That seemed
strange to me. Alternatively I looked at their Chapter summaries.
Chapter 15's title is 'Quantum Theory and the Implicate Order.'
In that chapter they omnistinguish classical Cartesian static
'order' from a much needed, and newer dynamic and evolving quantum~order.
As I was reading, it dawned on me (something as simple as this
prior escaped my attention) that Prigogine and Stenger's book's
title is Order Out of Chaos. Then I tried substitution
as my usual intuitive habit as Equilibrium Out of Chaos.
More... Quantum Theory of the Implicate Equilibrium. Those
substitutions appear quasi relevant in Doug's search for new
ways to ponder quantum vav classical issues of equilibrium.
Some huge philosophical issues emerge here. Is quantum~order
hyper quantum~equilibrium. Does order have higher Value
than equilibrium? Is high~rate change of equilibrium analogous
disorder? Is that classical 'di'sorder? Is that quantum~disorder?
Could we better describe it as high rate evolution of
equilibrium? See? 'Disorder' is a dichon.
Quantum remediation requires that we QELR
it as omnisorder, perhaps omnisorderings. If we make 'order'
hyper 'equilibrium' it appears to Doug that our memes
of order must encompass equilibrium, equilibria, and all their
unlimited and vast ephemeral variations. Should we allow quantum~equilibria
to encompass semantically and heuristically all its potential
holographic manifesta?
Then, what would we mean by "quantum~order?" Until
now, Doug had tended to keep 'order' and 'equilibrium' autsimilar
one another. Does that make any sense? Why? What do we mean by
'disequilibrium?' Should we QELR it "omnisequilibria?"
Now similarly use your noodle to ponder issues surrounding 'stability,'
'coherence,' 'quiescence,' 'stochastic modality,' 'chaotic attractors,'
etc. (Read Gleick's Chaos on 'chaotic attraction.') Doug
- 24Sep2011.
Bohm and Hiley agree with Doug's approach that a Cartesian
model of order (and apparently of equilibrium) is simply bogus
and no longer adequate.
They seek a new way of m¤daling both quantum~¤rdær
and (via Doug's inference) quantum~equilibrium (compare quantum~omnisequilibrium).
We see Doug's previously claimed need for omniscrimination
(classical vis-à-vis quantum) rearing its head right here
in Bohm and Hiley's (quantum~cosmic) River City.
Doug had another glimmer earlier: equilibrium issi
quanton(FFE,NTE). Try as I might, I cann¤t find anything
proemially inadequate with that script except its incompleteness
which I take as a given. But one meme stands out: dichon(FFE,
NTE) radically omniffers quanton(FFE,NTE)! What makes this fascinating
for Doug is how classical FFE
and NTE omniffer
quantum FFE and NTE. And we may choose to take that further:
classical quiescence omniffers quantum~quiescence. See NTQ.
So what is going on here?
What do classicists mean by 'order?' If a system has 'order,'
what does that mean classically? One answer is, "It is stable."
Classically order has stability and stability implies state under
classical assumptions of reality's linear motion as stoppable.
So a classical system which possesses order and stability as
canonic properties is linear and stoppable (both
necessary to do valid and verifiable classical analysis
and measurement of said system).
Hopefully you are keeping pace here. Quantum~systems are n¤t
canonically linear n¤r stoppable! Quantization and scintillation
are perpetually stochastic nonlinear processings: positive
wave energyings!
What Doug has just accomplished is to show that when we talk
about classical terms like order, stability, and equilibrium
our interpretations vastly omniffer what we can say and write
about quantum~order, ~stability, and ~equilibrium.
You may choose to see here how classicists have oversimplified
their models of reality by assuming (conventionally and conveniently)
reality is state-ic and stoppable.
Classical 'order' is already, by assumption, static. Ditto
stability and equilibrium.
When we talk and write about quantum~order, ~stability, and
~equilibria, we are assuming a wave~based perpetually changing
and evolving reality.
So we assess quantum~FFE, ~NTE, and NTQ using gradience of
flux autsimilarity evolutionings. See Doug's Assess
Resemblance HotMeme™. We assume absolute change,
selective choice at up to Planck rates, and chance as stochastics
borne of uncertaintyings of quantization and scintillation of
all quantum reality.
Our apparently remaining challenge is to describe quantum~order,
~stability, and ~equilibria using those assumptions as a radical
departure from classical approaches.
Doug will attempt that under a separate web page titled accordingly.
End 22-24Sep2011 Equilibrium Update.
This QELR of equilibria and equilibrium is in progress
until further notice - Doug - 20,22,24-30Mar2011 and 1,5,10,12-13,15-16,20-21,24Apr2011,
1-13Sep2011.
Page top index.
|